Devlog 2 - Jump Arcs
Published: May 25th, 2021
I spent some time yesterday refactoring and refining the jump mechanics for Rhythm Quest and thought I'd write a bit about it, since it's more interesting than it might seem at first blush.
In Rhythm Quest, each (normal) jump is roughly one beat in length. The exact horizontal distance varies, though, since the scroll rate is different for each song (and even within a song).
The naive approach
Your first instinct when implementing something like this might be to use simple platformer-style tracking of vertical velocity and acceleration:
void Jump() {
yVelocity = kJumpVelocity;
}
void FrameUpdate(float deltaTime) {
yVelocity += kGravityConstant * deltaTime;
yPosition += yVelocity * deltaTime;
}
Here we're essentially using a "semi-implicit euler integration", where we modify the differential velocity and position at each timestep. Surprisingly, it's actually fairly important that we modify the velocity before the position and not the other way around! See https://gafferongames.com/post/integration_basics/ for more on this.
There are a number of issues with this approach. Probably the biggest one is that the behavior is different depending on the framerate (deltaTime), which means that the jump will behave differently depending on the FPS of the game! You can fix that by using a fixed timestep to do this physics calculation instead of a variable timestep (Unity and Godot both provide a FixedUpdate physics processing step for this purpose).
The other problem is one that's specific to Rhythm Quest...
The problem
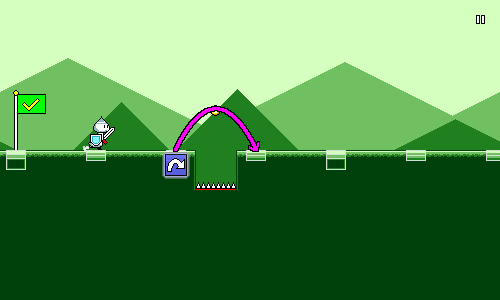
So after some algebra (or trial and error), we have our jump velocity and gravity figured out. The jump paths look something like this:
That's all fine and good, but when we add height changes into the mix, it's a different story:
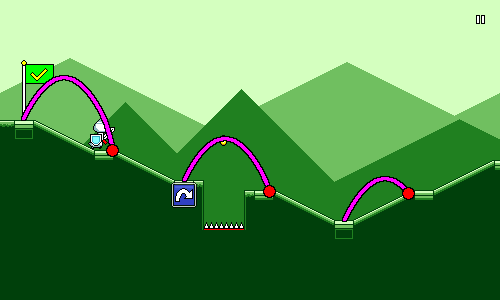
The sloping ramps in Rhythm Quest aren't actually supposed to have any bearing on gameplay -- they're mostly there for visual interest and to accentuate the phrasing of the music (it looks a lot more interesting than just running across an entirely flat plain). But they're actually causing gameplay issues now, since they throw off the duration of each jump. It might not seem like much, but it can add up and cause mistakes, especially in sections like this:
The above gif looks perfectly-aligned though, because it's using a better and robust solution. How did I manage to dynamically alter the jumping behavior to match the changing platform heights?
A more robust solution
The first thing we need to do is throw out our ideas of having a predetermined/fixed jump arc, since that obviously didn't work. Instead, we're going to calculate each jump arc dynamically. No trial-and-error here, we're going to use quadratics!
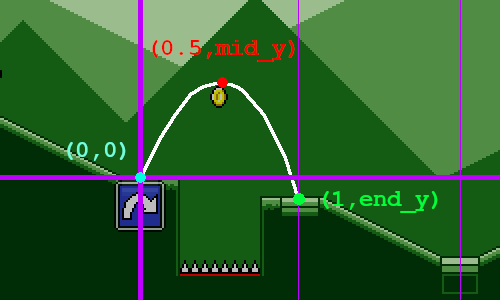
The fundamental equation for a parabolic / ballistic arc trajectory is given by y = ax^2 + bx + c. If we assume a start position of x = 0 and y = 0 (this would be the start of the jump), then we can simplify that to y = ax^2 + bx.
In other words, if we know the two constants a and b, then we can just plug them into this equation and have a mapping between y and x which will trace out an arc. a here represents our "gravity" term and b represents our initial velocity.
Since we have two unknowns (a and b), we can solve for them if we're given two nonzero points. In other words, we just need to pick two points along the path of the jump arc, and then we can solve the algebra and have a formula that we can use to calculate our y-coordinates.
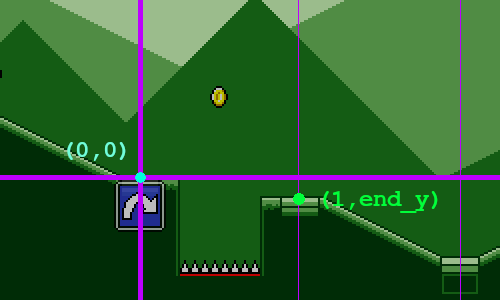
The whole idea of this exercise is to have the player land exactly on the target position at the end of the jump, so let's pencil that in as one of our points (shown here in green). To make our lives easier, we'll say that the x-coordinate at this point is 1:
Of course, in order for this to work, we need to know exactly what end_y is. We could try to calculate this using a raycast, but that wouldn't work if your jump "landing" position isn't actually on the ground (e.g. you mis-timed a jump and are going to fall into a pit!).
Instead the way that this works is that I have a series of "ground points" that are generated on level initialization. These form a simple graph of the "ground height" of the level, minus any obstacles. This lets me easily query for the "ground height" at any x-coordinate by using linear interpolation. Conceptually it looks like this:
For our third point, let's just have that be in the middle of the jump horizontally.
There are a couple of different options we could use for determining mid_y, the height of this point. Here's what I ended up with after some twiddling around:
// Some constant base jump height.
float midHeight = GameController.JumpHeight;
if (yDiff > 0.0f) {
// The end of the jump is higher than the beginning.
// Bias towards jumping higher since that looks more natural.
midHeight += yDiff * 0.5f;
} else {
// The end of the jump is lower than the beginning.
// Here I bias towards jumping lower, but not as much as above.
// It ends up looking a bit more natural this way.
midHeight += yDiff * 0.25f;
}
Time for some math
We have all of our variables and knowns, so let's actually do the math now! We have two equations that we get from plugging in our two points into the basic formula y = ax^2 + bx:
mid_y = 0.25a + 0.5b // x = 0.5, y = mid_y end_y = a + b // x = 1, y = end_y
This is extremely easy to solve -- just multiply the top equation by two and take the difference. In the end we get:
a = 2 * end_y - 4 * mid_y b = end_y - a
Now that we know a and b, we can store them and then use them to trace out the path of the arc!
So to wrap it up, each time the player presses jump, we:
- Store the beginning x-coordinate and y-coordinate
- Calculate a and b as shown above
- On subsequent frames, set y = ax^2 + bx + starting_y
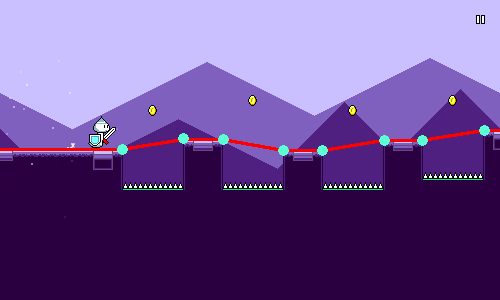
The end result, once more:
This is way better than our naive solution from the beginning of the article. Not only does it work with varying heights, but we derived an exact equation to trace out our jump arc (no approximations!), which means we can just update the visual x and y coordinates in the rendering update instead of having to deal with physics-based timesteps.
A few extra things I also ended up doing to make the jumps feel better:
First, I made jumps actually last slightly shorter than one beat. This is because it looks more natural to have a short period where the character has definitively landed on the ground before the next jump. This also allows for some more leeway for timing consecutive jumps, and ensures that timing errors don't compound unfairly.
I also allow for early jumps -- in other words, you can re-jump slightly before you actually touch the ground. This again helps with ensuring that timing errors don't compound, and is a nice quality-of-life improvement for players. In this case I make sure to "snap" your y-coordinate downwards at the beginning of the jump, so it still looks as if you ended up touching the ground (even though you didn't really).
<< Back: Devlog 1 - Welcome to Rhythm Quest
>> Next: Devlog 3 - Flying Mechanic and Level Generation